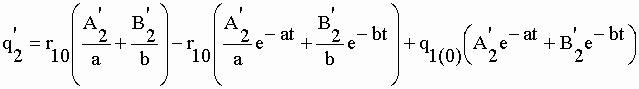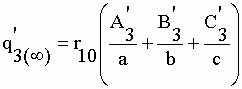Chapitre II Etude des systèmes et modélisation |
|||
| IV. Méthode de l'infusion constante du marqueur (suite et fin) | |||
| Lorsqu'il s'agit d'un système à plusieurs compartiments la cinétique de perfusion apparaît plus compliquée. L'évolution de la concentration du marqueur dans le compartiment central résulte non seulement de la perfusion et de l'élimination définitive du marqueur, mais aussi des échanges entre les compartiments central et périphériques. Il y a équilibre dans tous les compartiments lorsque le flux d'élimination du marqueur est rigoureusement identique au flux de perfusion. Dans ce cas l'intérêt essentiel de la méthode est de pouvoir déterminer les pools de substances endogènes dans les tissus peu accessibles lorsque l'on estime que l'équilibre entre marqueur et marqué est à peu près atteint dans l'ensemble du système. La transformation de Laplace est une fois de plus très efficace pour intégrer le réseau d'équations différentielles linéaires du modèle mathématiques. Examinons un système à 2 compartiments que l'on perfuse par IV (Fig. II-14). | |||
Figure II-14 : Système à 2 compartiments avec perfusion continue "r10" de marqueur. R10 représente le flux d'entrée du marqué dans le compartiment 1. |
|
||
| Les équations II-39 à 50 correspondant à un modèle à 2 compartiments avec injection unique de marqueur ne sont que légèrement modifiées par l'introduction du taux de perfusion "r10" : | |||
| dq'1/dt
= r10 –
K1 q'1
+ k12 q'2
dq'2/dt = +k21 q'1 – K2 q'2 |
II-134 | ||
| s.F'1
– q1(0)
= r10/s
– K1 F'1
+ k12 F'2
s.F'2 – q2(0) = +k21 F'1 – K2 F'2 |
II-135 | ||
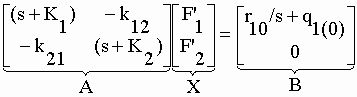 |
II-136 | ||
| où
q1(0) = q'2(0) = 0. Si, comme plus
haut, une dose de charge est injecte au début de la
perfusion on a q1(0)>0. La matrice carrée
"|A|" étant identique à celle de l'équation
II-41, son déterminant |A| (éq. II-42) et les
expressions correspondantes de x et y (éq.II-43) sont
utilisés sans changements ici. Sans dose de charge (q1(0) = 0) nous avons les transformées de Laplace : |
|||
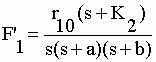
|
II-137 | ||
| avec 3 pôles "sp" (s1 = 0, s2 = -b et s3 = -a ). Chacune des fonctions f1(t) = q'1 et f2(t) = q'2 est donc la somme de 3 résidus. Concernant la fonction q'1 : | |||
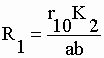 , pour s1 = 0 ; , pour s1 = 0 ;
|
II-138 | ||
| Désignons les rapports contenus dans les résidus par : | |||
| A'1
= (K2 – a) / (b – a) B'1 = (K2 – b) / (a – b) |
II-139 | ||
| de sorte que A'1 + B'1 = 1. En combinant les résidus (éq.II-138) avec les expressions de A'1 et B'1 (éq. II-139) et en divisant par le volume V1 on obtient la concentration "c'1" de marqueur dans le compartiment central : | |||
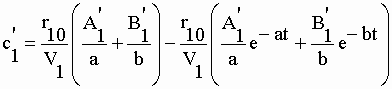 |
II-140 | ||
| A l'équilibre, c'est-à-dire à t = ¥ , les deux termes "e-at" et "e-bt" s'annulent de sorte que : | |||
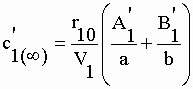 |
II-141 | ||
| De la même manière, la fonction f2(t) = q'2 est obtenue à partir de la transformée F'2 (éq. II-137) : | |||
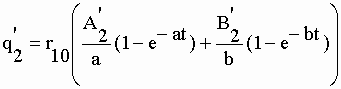 |
II-142 | ||
| où : | |||
| A'2
= k21 / (b -
a) B'2 = k21 / (a - b) |
II-143 | ||
| de sorte que A'2 + B'2 = 0. A l'équilibre, pour t = ¥ : | |||
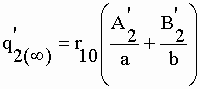 |
II-144 | ||
| On peut vérifier que les asymptotes "c'1(¥ ) et q'2(¥ )" (éq. II-141et II-144), pour un taux de perfusion r10 donné, sont prévisibles en utilisant les AUCs (éq. II-72) déterminées lors de l'analyse après injection unique de marqueur : | |||
| c'1(¥ )
= r10 AUC1
/ 100 q'2(¥ ) = r10 AUC2 / 100 |
II-145 | ||
| où les indices 1 et 2 des AUCs désignent respectivement le compartiment central et le compartiment périphérique. En effet, les expressions A'1 et B'1 (éq. II-139) et A'2 et B'2 (éq. II-143) ne diffèrent des coefficients exponentiels respectifs A1 et B1 (éq. II-48) et A2 et B2 (éq. II-50) que par le facteur q1(0) (= 100 % de la dose unique de marqueur injecté). A l'inverse, on peut estimer r10 en conformité avec le niveau d'équilibre souhaité : | |||
| r10 = 100 c'1(¥ ) / AUC1 = 100 q'2(¥ ) / AUC2 | II-146 | ||
| Si une dose de charge q1(0) égale à q'1(¥ ) est administrée au début de la perfusion, la concentration d'équilibre c'1(¥ ) dans le compartiment central est atteinte d'emblée. On peut démontrer comme plus haut que c'1 et q'2 sont des sommes de la cinétique de perfusion et de la cinétique après injection unique de marqueur : | |||
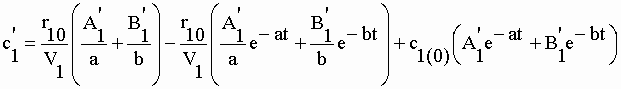
|
II-147 | ||
| Exercice : Infusion constante d'un marqueur avec ou sans dose de charge (2 compartiments) | |||
| Complétons et illustrons les cas de perfusion de systèmes multi-compartimentaux par l'exemple du système eau à 3 compartiments (Fig. II-1 et 6 ; eq. II-95)) dans lequel on perfuse de l'eau tritiée par voie intraveineuse à raison de 1500 dpm / heure. Les transformées de Laplace "F'1, F'2 et F'3" des quantités de marqueur "q'1, q'2 et q'3" sont identiques aux transformées de Laplace "F1, F2 et F3" des équations II-26 à 28 excepté l'introduction ici de "r10 / s". Les expressions symboliques des coefficients A'1, B'1 et C'1 sont déduites des équations II-34 : | |||
| A'1
= [(K2 –
a) (K3
– a) – k23 k32]
/ [(b – a)(c – a)] B'1 = [(K2 – b) (K3 – b) – k23 k32] / [(a – b)(c – b)] C'1 = [(K2 – c) (K3 – c) – k23 k32] / [(a – c)(b – c)] |
II-148 | ||
| ce qui, pour une perfusion sans dose de charge, nous amène à : | |||
 |
II-149 | ||
| A l'équilibre, pour t = ¥ : | |||
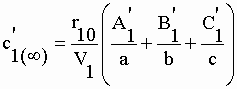 |
II-150 | ||
| Les coefficients concernant les quantités de marqueur q'2 et q'3 dans les compartiments 2 et 3 sont : | |||
| A'2
= k21 (K3
– a) / [(b – a)(c – a)] B'2 = k21 (K3 – b) / [(a – b)(c – b)] C'2 = k21 (K3 – c) / [(a – c)(b – c)] A'3 = k21 k32 / [(b – a)(c – a)] B'3 = k21 k32 / [(a – b)(c – b)] C'3 = k21 k32 / [(a – c)(b – c)] |
II-151 | ||
| On en tire les expressions pour les quantités de marqueur dans les compartiments périphériques : | |||
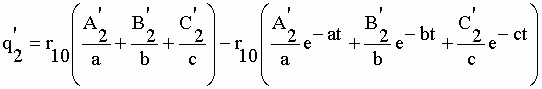
|
II-152 | ||
| A l'équilibre : | |||
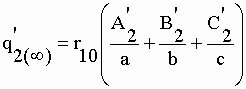
|
II-153 | ||
| De la même manière que dans le cas d'un système à 2 compartiments (éq.II-145) les asymptotes "c'1(¥ ), q'2(¥ ) et q'3(¥ )" (éq. II-150 et II-153) sont prévisibles à partir des AUCs déterminées lors de l'analyse après injection unique de marqueur : | |||
| c'1(¥ )
= r10 AUC1
/ 100 q'2(¥ ) = r10 AUC2 / 100 q'3(¥ ) = r10 AUC3 / 100 |
II-154 | ||
| L'indice
des AUCs fait référence au compartiment concerné. Pour
le système eau à 3 compartiments après injection
unique de marqueur (Tab. II-3) AUC1 = 833,333
%.heure / litre, AUC2 = 10000 %.heure et AUC3
= 20833,333 %.heure (pour la méthode de calcul voir éq.
II-73 et 74). Le taux de perfusion est donc ajustable en
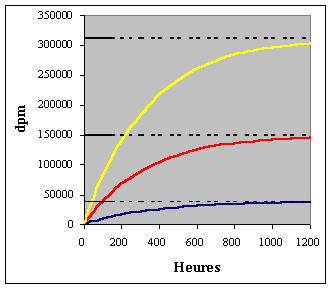
fonction du niveau d'équilibre isotopique souhaité. La figure II-15 montre l'évolution de la quantité d'eau tritiée dans chaque compartiment du système pendant la perfusion du marqueur sans dose de charge pour r10 = 1500 dpm / heure. Les courbes ont pour équations : |
|||
| c'1
= 12500 - 5,987e-65,61t
- 19,88e-3,49t
- 12474e-0,002994t q'2 = 150000 + 18,75e-65,61t - 223,9e-3,49t - 149795e-0,002994t q'3 = 312500 - 0,8021e-65,61t + 283,0e-3,49t - 312782e-0,002994t |
II-155 | ||
| Les valeurs asymptotiques sont proportionnelles aux volumes des compartiments (voir Fig. II-1), ce qui est logique dans la mesure où la concentration en eau tritiée et la radioactivité spécifique de l'eau à l'équilibre sont homogènes dans tout le système. | |||
Figure II-15 : Evolution en fonction du temps des quantités d'eau tritiée dans les compartiments plasmatique, interstitiel et cellulaire (de bas en haut) au cours d'une perfusion de marqueur par IV (r10 = 1500 dpm par heure). Les lignes en pointillé indiquent les quantités asymptotiques q'1(¥ ) = 37500 dpm, q'2(¥ ) = 150000 dpm et q'3(¥ ) = 312500 dpm (de bas en haut) atteintes au temps t = ¥ . |
|
||
| Il
faudrait environ 6 semaines (1000 heures) pour que q'1,
q'2 et q'3 atteignent 95 % de la
valeur d'équilibre au temps t = ¥ et prés de 11
semaines (1800 heures) pour dépasser 99 %.
L'administration d'une dose de charge judicieusement
choisie permet de réduire considérablement ces délais.
Il suffit de 3 heures de perfusion, avec une dose de
charge égale à la quantité totale de marqueur dans le
système à l'équilibre (q'1(¥ ) + q'2(¥ ) + q'3(¥ ) ) pour que la valeur
d'équilibre dans chaque compartiment soient approchées
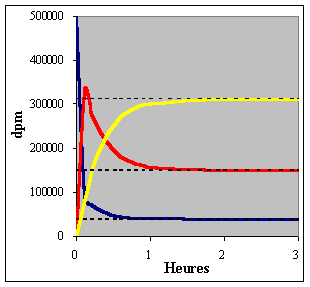
à 99,8 % (Fig. II-16). Les courbes de la figure II-16 ont pour équations : |
|||
| c'1
= 12500 + 130944e-65,61t
+ 23248e-3,49t
- 25,89 e-0,002994t q'2 = 150000 - 410136e-65,61t + 260447e-3,49t - 310,9e-0,002994t q'3 = 312500 + 17543e-65,61t - 329394e-3,49t - 649,2e-0,002994t |
II-156 | ||
| Il est important de noter que la dose de charge dans un système multi-compartimental peut entraîner des pics élevés de substance dans les compartiments avant que l'équilibre ne soit atteint (Fig. II-16). Cet effet transitoire peut être néfaste pour l'organisme si les pics dépassent les seuils de toxicité. | |||
| Exercice : Infusion constante d'un marqueur avec ou sans dose de charge (3 compartiments) | |||
Figure II-16 : Evolution des quantités d'eau tritiée dans les compartiments plasmatique, interstitiel et cellulaire (de bas en haut) au cours des premières heures de perfusion du marqueur par IV (r10 = 1500 dpm par heure) avec dose de charge (q1(0) = 500000 dpm). Les lignes en pointillé indiquent les quantités à l'équilibre q'1(¥ ) = 37500 dpm, q'2(¥ ) = 150000 dpm et q'3(¥ ) = 312500 dpm (de bas en haut). |
|
||
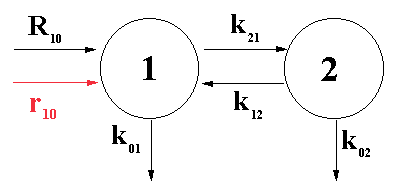

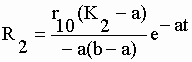 , pour s2 =
-a ;
, pour s2 =
-a ;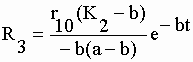 , pour s3 = -b.
, pour s3 = -b.