Chapitre II
Etude des systèmes et modélisation |
| |
|
|
|
|
| II. Elaboration des modèles
mathématiques |
| |
|
|
|
|
| a- Equations
différentielles linéaires. Pour tout
modèle théorique la première étape consiste à poser le réseau d’équations
différentielles linéaires décrivant le système. Reprenons notre modèle à 3
compartiments de l’eau corporelle : |
| |
|
|
|
|
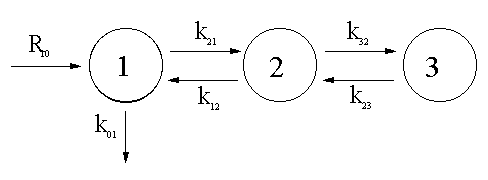
Figure
II-6 : Modèle théorique du métabolisme de l’eau corporelle. |
 |
| |
|
|
|
|
|
| Après injection
d’une dose unique de 3H2O dans le compartiment 1 (central) par
voie IV, la variation de la quantité de marqueur dans chaque compartiment en fonction du
temps est exprimée par un réseau d’équations différentielles linéaires qui
constitue le modèle mathématique du système : |
|
|
|
|
|
dq1/dt
= -K1q1 + k12q2 > 0 dq2/dt = +k21q1 -K2q2
+ k23q3 > 0
dq3/dt = +k32q2
-K3q3 > 0 |
II-17 |
|
|
|
|
| Ce qui entre dans un
compartiment est compté comme positif, ce qui en sort comme négatif. K1
= (k01 + k21), K2 = (k12 + k32), K3
= k23. Parce que les contenus en 3H2O diminuent en
fonction du temps, ce système est dit en état non stationnaire. Si l’on considère les mouvements de l’eau non
radioactive : |
|
|
|
|
|
dQ1/dt
= +R10 -K1Q1 + k12Q2 = 0 dQ2/dt = +k21Q1 -K2Q2
+ k23Q3 = 0
dQ3/dt = +k31Q2
–K3Q3 = 0 |
II-18 |
|
|
|
|
| Dans ce cas, les
variations de Q1, Q2 et Q3 sont nulles. On dit que ce
système est en état stationnaire car, pour chaque compartiment, la somme des
entrées (+) compense la somme des sorties (-). K1, K2 et K3
représentent dans ce cas les constantes de renouvellement des compartiments 1, 2 et 3. Dans l’analyse de flux de substances endogènes,
telles que l’eau, caractérisées par le renouvellement, sont superposés un système
en état stationnaire (eau non radioactive) et un système en état non stationnaire (3H2O),
ce dernier permettant d’estimer les paramètres du premier. |
|
|
|
|
|
| b- Transformations
de Laplace. Le suivi de l’état
du système pendant toute la durée de l’analyse nécessite l’intégration des
équations différentielles linéaires du modèle mathématique (équations II-17) pour
obtenir les équations pratiques des courbes expérimentales.
Il est facile d’intégrer l’équation
différentielle linéaire d’un système à un compartiment tel que celui de
l’eau à partir de 6 heures après injection de 3H2O (voir
chap. I, éq. I-61 et 62) : |
|
|
|
|
|
dq1/dt
= -k01q1 q1 = q1(0)e-k01t |
II-19 |
|
|
|
|
| où la quantité q1
de marqueur est exprimée en % de la dose injectée au temps "t" et q1(0)
est égal à 100 % de la dose injectée (q1 pour t = 0). Poursuivons l’application pour le modèle eau à 3
compartiments marquée par 3H2O dont le réseau
d’équations différentielles linéaires du modèle mathématique a été construit
antérieurement (équations II-17) : |
|
|
|
|
|
dq1/dt
= -K1q1 + k12q2 dq2/dt = +k21q1 -K2q2
+ k23q3
dq3/dt = +k32q2
-K3q3 |
|
|
|
|
|
| L’étape suivante
consiste à effectuer les transformées de Laplace de ce réseau d’équations en
suivant les indications des paragraphes précédents : |
|
|
|
|
|
sF1
– q1(0) = -K1F1 + k12F2 sF2 – q2(0) = +k21F1
-K2F2 + k23F3
sF3 – q3(0) =
+k32F2 -K3F3 |
II-20 |
|
|
|
|
| où q1(0) =
1 soit 100 % de la dose injectée, q2(0) = q3(0) = 0. Arrangeons ces équations en réseau matriciel pour
obtenir les transformées F1, F2 et F3 correspondant aux
fonctions f1(t) = q1, f2(t) = q2 et f3(t)
= q3 : |
| |
|
|
|
|
|
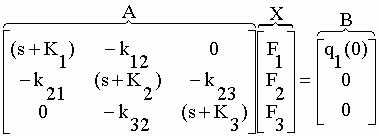 |
II-21 |
| |
|
|
|
|
|
|
| La règle de Cramer
(voir chap. I) permet d’établir les transformées de Laplace F1, F2
et F3 : |
| |
|
|
|
|
|
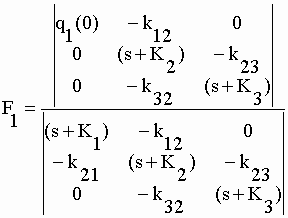 |
II-22 |
| |
|
|
|
|
|
|
| Le déterminant de la
matrice |A| au dénominateur est égal à : |
|
|
|
|
|
s3 +
s2 (K1 + K2 + K3) + s(K1K2
+ K2K3 + K1K3 – k12k21
- k23k32) + K1K2K3 – K1k23k32
- K3k12k21 |
II-23 |
|
|
|
|
| Il s’agit
d’une expression cubique du type : |
|
|
|
|
|
(s + a) (s + b)
(s + c) = s3 + s2 (a + b + c) + s (ab + ac + bc) + abc |
II-24 |
|
|
|
|
| En combinant les
équations II-23 et II-24 nous posons : |
|
|
|
|
|
x = a + b + c =
K1 + K2 + K3 y = ab + bc+ ac = K1K2 + K2K3
+ K1K3 – (k12k21 + k23k32)
z = abc = K1K2K3
– (K1k23k32 + K3k12k21) |
II-25 |
|
|
|
|
| Par conséquent : |
|
|
|
|
|
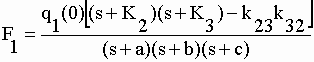 |
II-26 |
|
|
|
|
| En substituant le
vecteur B [q1(0), 0, 0] à la 2ème puis à la 3ème
colonne du numérateur on obtient successivement les deux autres transformées : |
|
|
|
|
|
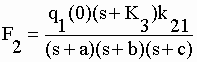 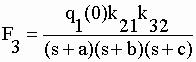
|
II-27 II-28 |
|
|
|
|
| Chacune de ces
transformées a 3 pôles sp (s1 = -a, s2 = -b et s3
= -c). La transformation inverse de la transformée de Laplace F1 nous permet
d’obtenir la fonction f1(t) = q1 (% de la dose dans le
compartiment 1 au temps t). La fonction f1(t) = q1 est la somme de 3
résidus (R1 + R2 + R3) : |
|
|
|
|
|
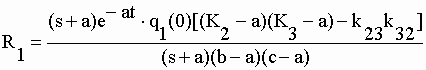 , pour s1= -a , pour s1= -a |
II-29 |
|
|
|
|
| où les termes
"(s+a)" sont éliminés au numérateur et au dénominateur et les "s"
restant remplacés par "–a", ce qui donne le premier résidu : |
|
|
|
|
|
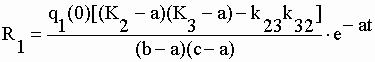 |
II-30 |
|
|
|
|
| qui est aussi
l’expression développée de la première exponentielle de f1(t) = q1.
Les deux autres résidus sont obtenus de la même manière. |
|
|
|
|
|
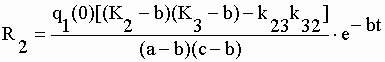 , pour s2 =
-b , pour s2 =
-b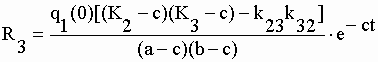 , pour s3 = -c , pour s3 = -c
|
II-31 II-32 |
|
|
|
|
| Dans la pratique les
données expérimentales sont des concentrations plasmatiques "c1"
exprimées en % de la dose injectée par unité de volume équivalent de plasma de sorte
que le volume "V1" du compartiment est inclus dans la formule.
Puisque V1 = q1(0) / c1(0),
R1/V1 = A1.e-at,
R2/V1 = B1.e-bt et R3/V1
= C1.e-ct. La concentration plasmatique en marqueur c1 est
alors : |
|
|
|
|
|
c1 =
A1 e-at + B1 e-bt + C1 e-ct |
II-33 |
|
|
|
|
| où |
|
|
|
|
|
A1 =
c1(0) [(K2 – a) (K3 – a) – k23 k32]
/ [(b – a)(c – a)] B1 = c1(0) [(K2 – b) (K3
– b) – k23 k32] / [(a – b)(c – b)]
C1 = c1(0) [(K2
– c) (K3 – c) – k23 k32] / [(a
– c)(b – c)] |
II-34 |
|
|
|
|
| Les coefficients
exponentiels des équations pour q2 et q3 sont obtenus de la même
manière que pour ceux de q1 : |
|
|
|
|
|
A2 =
q1(0) k21 (K3 – a) / [(b – a)(c – a)] B2 = q1(0) k21 (K3
– b) / [(a – b)(c – b)]
C2 = q1(0) (0) k21
(K3 – c) / [(a – c)(b – c)] |
II-35 |
|
|
|
|
|
A3 =
q1(0) k21 k32 / [(b – a)(c – a)] B3 = q1(0) k21 k32
/ [(a – b)(c – b)]
C3 = q1(0) k21
k32 / [(a – c)(b – c)] |
II-36 |
|
|
|
|
|
q2 =
A2 e-at + B2 e-bt + C2 e-ct
q3 = A3 e-at
+ B3 e-bt + C3 e-ct |
II-37 II-38 |
|
|
|
|
| L’élaboration du
modèle mathématique pour le système eau réduit à deux compartiments procède
de la même technique mais les calculs sont évidemment moins longs : |
|
|
|
|
|
dq1/dt
= -K1q1 + k12q2 dq2/dt = +k21q1
-K2q2 |
II-39 |
|
|
|
|
|
sF1
– q1(0) = -K1F1 + k12F2 sF2 – q2(0) = +k21 F1
-K2 F2 |
II-40 |
|
|
|
|
| où q1(0) =
100 % de la dose injectée et q2(0) = 0. |
| |
|
|
|
|
|
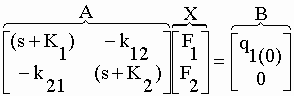 |
II-41 |
| |
|
|
|
|
|
|
| Avec le déterminant de
la matrice carrée "|A|" on obtient l’équation simplifiée : |
|
|
|
|
|
(s + a) (s + b)
= s2 +s (a + b) + ab |
II-42 |
|
|
|
|
| de telle sorte
que : |
|
|
|
|
|
x = a + b = K1 +
K2 y = ab = K1K2
– k12k21 |
II-43 |
|
|
|
|
| Les transformées de Laplace : |
|
|
|
|
|
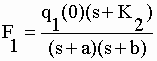 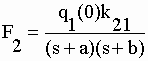
|
II-44 II-45 |
|
|
|
|
| ont chacune 2 pôles "sp"
(s1 = -a et s2 = -b). Chacune des fonctions f1(t) =
q1 et f2(t) = q2 est la somme de 2 résidus "R1
+ R2". En ce qui concerne
la fonction q1 : |
|
|
|
|
|
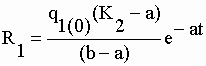 , pour s1 = -a , pour s1 = -a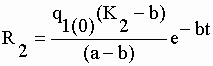 ,
pour s2 = -b ,
pour s2 = -b
|
II-46 |
|
|
|
|
| De la même manière que pour le
modèle à 3 compartiments l’équation des concentrations plasmatiques : |
|
|
|
|
|
c1 = A1 e-at
+ B1 e-bt |
II-47 |
|
|
|
|
| où : |
|
|
|
|
|
|
|
|
A1 = c1(0)
(K2 – a) / (b – a) B1 = c1(0) (K2 – b) / (a
– b) |
II-48 |
|
|
|
|
| La fonction f2(t) : |
|
|
|
|
|
q2 = A2 e-at
+ B2 e-bt |
II-49 |
|
|
|
|
| où : |
|
|
|
|
|
|
|
|
A2 = q1(0)
k21 / [(b - a)(c - a)] B2 = q1(0) k21 / [(a - b)(c - b)] |
II-50 |
| |
|
|
|
|
|
|
|
 
RETOUR AU SOMMAIRE |